Introduction

If you shoot a cannon, how far will the cannon ball go before it hits the ground? How high will it go?

Design

1. All input and output data is in feet/seconds/degrees
2. The acceleration of gravity is 32 feet/sec/sec (9.8 meters/sec/sec)
3. There is no air resistance to slow the cannonball
4. The earth is flat (no curvature)
5. Ignore the rotation of the earth
6. Ask the user for:
   • The cannon's angle above the horizon
     Do not allow angles less that 20° or greater than 90°
   • The muzzle velocity of the cannon
     Do not allow velocities (less that 10 feet/sec or greater than 2000 feet/sec?)
7. Display
   • Cannonball flight time (seconds)
   • Horizontal distance traveled (feet)
   • Maximum vertical distance (feet)

Calculation

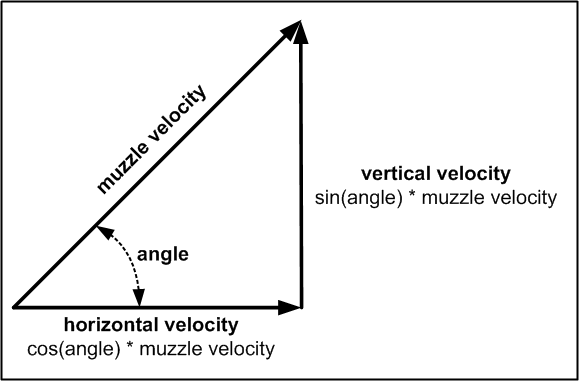
Input

Vm                  // muzzle velocity (feet/sec)
A                   // cannon elevation angle (degrees)

Horizontal and Vertical Velocity

Vv = sin(A) * Vm    // vertical velocity (feet/sec)
Vh = cos(A) * Vm    // horizontal velocity (feet/sec)

Note: Depending on which programming language you use, you may
need to convert angles in degrees to radians. For example,
the Python sin and cos functions require radians.

    Radians = Degrees x Pi / 180

    (Pi is approximately 3.14159)

    (1 radian is approximately 57.296 degrees)

    (1 degree is approximately 0.0174532925 radians)

Time (seconds) to the top of the arc (zero vertical velocity)

Ttop = Vv / 32.0

Note: 32.0 = acceleration of gravity (feet/sec/sec) 

Total time (seconds) of flight - up and then down

Ttotal = 2 * Ttop

Horizontal distance (feet)

Dh = Ttotal * Vh

Vertical distance (feet) to top of arc (zero vertical velocity)

Dv = (Vv)2 / (2 * 32.0)

Note: 32.0 = acceleration of gravity (feet/sec/sec) 

Note: Go here for more information on the calculation

Try This

Plot the cannonball's trajectory.