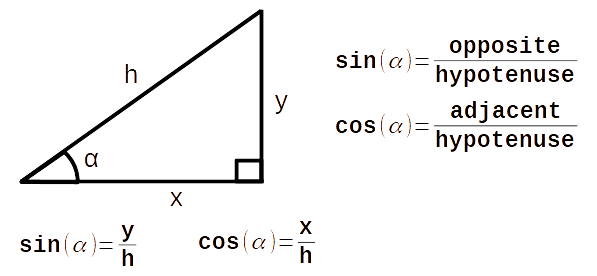Project #1

Assume that x is the height the tallest mast on a sail boat. Create a table of mast heights (10, 20, 30, 40, ..., 100) and how far a boat must sail (longitude/degrees) before the top of the mast is no longer visible.

Display the angle in degrees, minutes, seconds.

Project #2

Add to the table created in Project #1 how far the boat has sailed in feet, miles, nautical miles, meters, and/or kilometers.
Remember distance traveled is on the surface of the earth which is curved.

Project Assumptions and Equations

• the earth is a perfect sphere
• you can see clearly (haze does not effect seeing long distances)
• 3959 earth radius in miles
• 6371 earth radius in kilometers
• 24875.11 earth circumference in miles
• 40030.14 earth circumference in kilometers
• you are located on the prime meridian; you are on the equator looking directly west
  (This does not matter with a perfect sphere, but this will help clarify thinking.)

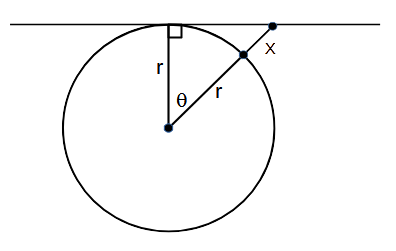
r	radius of the earth adjacent side of right triangle and angle θ
x	height of mast
r + x	hypotenuse of right triangle
θ	angle (at the equator it is a measure of east/west longitude)

Note: θ is an acute angles that is greater than 0° and less than 90°

import numpy as np

hypotenuse = r+x = r/np.cos(θ)

θ = np.arccos(r/(r+x))

Notes:
1. If (y/h) is the cosine of θ, then θ is the arc cosine of (y/h).
2. In Python the angles are measured in radians, not degrees.

What is Sine and Cosine