Introduction
Dijkstra's algorithm is a popular search algorithm used to determine the
shortest path between two nodes in a graph.
There are many examples of the algorithm on the web. If you don't like
Dijkstra's algorithm, modify it or create your own.
(Chewing on this problem is a great learning experience.)
Several projects can be found HERE
 .
.
Simple Cost Matrix
A small node-and-cost diagram (graph)
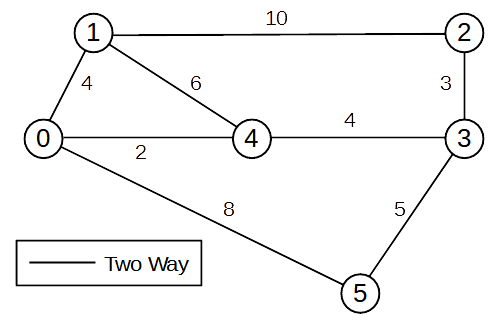
- cost could represent anything: travel time, travel distance, fuel use, congestion,
pollution, ...
- -1 indicates no direct node to node connection
- using this matrix, from->to and to->from costs can be different
- To find the cost between node A -> B
- pick a start node - column (node A)
- pick an end node - row (node B)
- find cost at matrix [row][column] i.e. [from-node][to-node]
- this matrix is used to create the minimum cost paths between nodes
# ---- node to node cost --------------------------------------
#
# [0] [1] [2] [3] [4] [5] (col is from-node)
#
costs = [ [ 0, 4, -1, -1, 2, 8 ], # row is to-node [0]
[ 4, 0, 10, -1, 6, -1 ], # row is to-node [1]
[ -1, 10, 0, 3, -1, -1 ], # row is to-node [2]
[ -1, -1, 3, 0, 4, 5 ], # row is to-node [3]
[ 2, 6, -1, 4, 0, -1 ], # row is to-node [4]
[ 8, -1, -1, 5, -1, 0 ] ] # row is to-node [5]
# ---- accumulated minimum path costs -------------------------
#
# [0] [1] [2] [3] [4] [5] (col is from-node)
#
accumulated_costs = [ [ 0, 4, 9, 6, 2, 8 ], # row is to-node [0]
[ 4, 0, 10, 10, 6, 12 ], # row is to-node [1]
[ 9, 10, 0, 3, 7, 8 ], # row is to-node [2]
[ 6, 10, 3, 0, 4, 5 ], # row is to-node [3]
[ 2, 6, 7, 4, 0, 9 ], # row is to-node [4]
[ 8, 12, 8, 5, 9, 0 ] ] # row is to-node [5]
Resultant Minimum Path Matrix
- pick a start node (from-node/column) and an end node (to-node/row)
- a value of -1 indicate the to-node and from-node are the same node
- in the to-node row, the value at [row,column] is the
next node (column) in the minimum path from start node to end node
- for example:
- the minimum path from node 3 to node 1 is 3 -> 4 -> 1
- the minimum path from node 2 to node 0 is 2 -> 3 -> 4 -> 0
# ---- minimum paths ------------------------------------------
#
# [0] [1] [2] [3] [4] [5] (col is from-node)
#
min_path = [ [ -1, 0, 3, 4, 0, 0 ], # row is to-node [0]
[ 1, -1, 1, 4, 1, 0 ], # row is to-node [1]
[ 4, 2, -1, 2, 3, 3 ], # row is to-node [2]
[ 4, 4, 3, -1, 3, 3 ], # row is to-node [3]
[ 1, 4, 3, 4, -1, 3 ], # row is to-node [4]
[ 5, 0, 3, 5, 3, -1 ] ] # row is to-node [5]
A More Compact Version of the Cost Matrix
Click HERE
 for more information.
for more information.
I use it because it is simpler to use and easier to modify.
And, you only have to work with outbound nodes
when designing a new cost matrix. (It can also be
easily converted to a regular 2D cost matrix.
Links
Python Program for Dijkstra's shortest path algorithm
Dijkstra's shortest path algorithm
A self learner’s guide to shortest path algorithms, with implementations in Python
Dijkstra's Algorithm
Dijkstra Algorithm in Python
Implementing Djikstra's Shortest Path Algorithm with Python
A* Pathfinding Visualization Tutorial - Python A* Path Finding Tutorial
(YouTube)
How Dijkstra's Algorithm Works
(YouTube)
 .
.

 for more information.
for more information.