Wikipedia - Golden Spiral

In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ (phi), the golden ratio.
That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes.

The equation for the golden ratio is:

Wikipedia - Golden Ratio

In mathematics, two quantities are in the golden ratio (φ or Φ) if their ratio is the same as the ratio of their sum to the larger of the two quantities.

Expressed algebraically, for quantities a and b with a > b > 0. Two quantities a and b are in the golden ratio φ (phi) if

Project #1

Draw a golden spiral in a 2D graphics window.

Use Cartesian coordinates.

The start point is 30 pixels along the +X axis. (0°)

Rotate counter-clockwise to draw the spiral.

Stop when the next point is outside the graphics window.

Use graphics.py. It is a simple graphics library. Click HERE for more information. (download, install, documentation, ...)

For example:

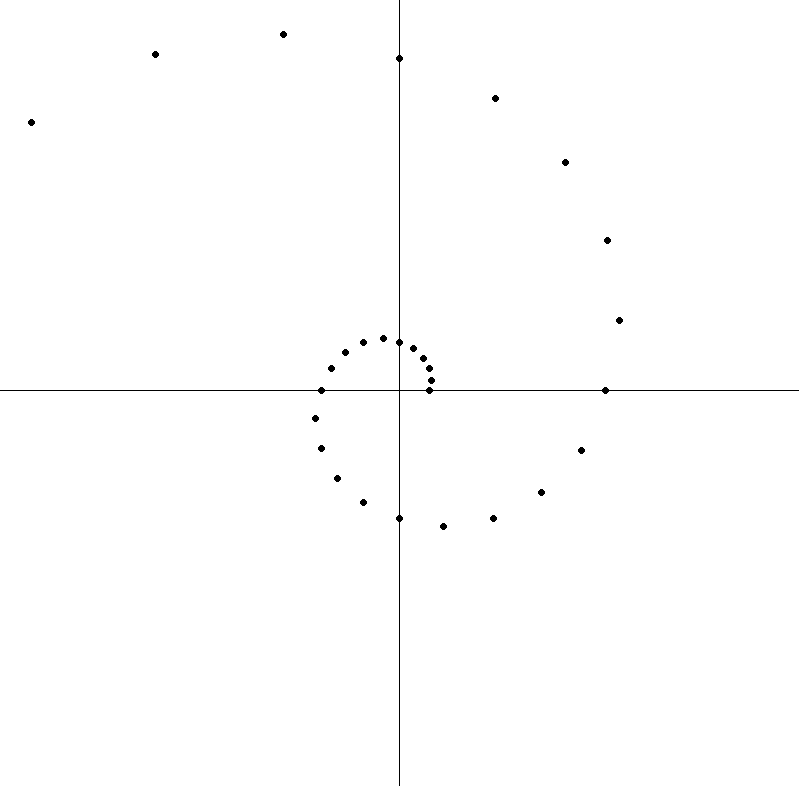
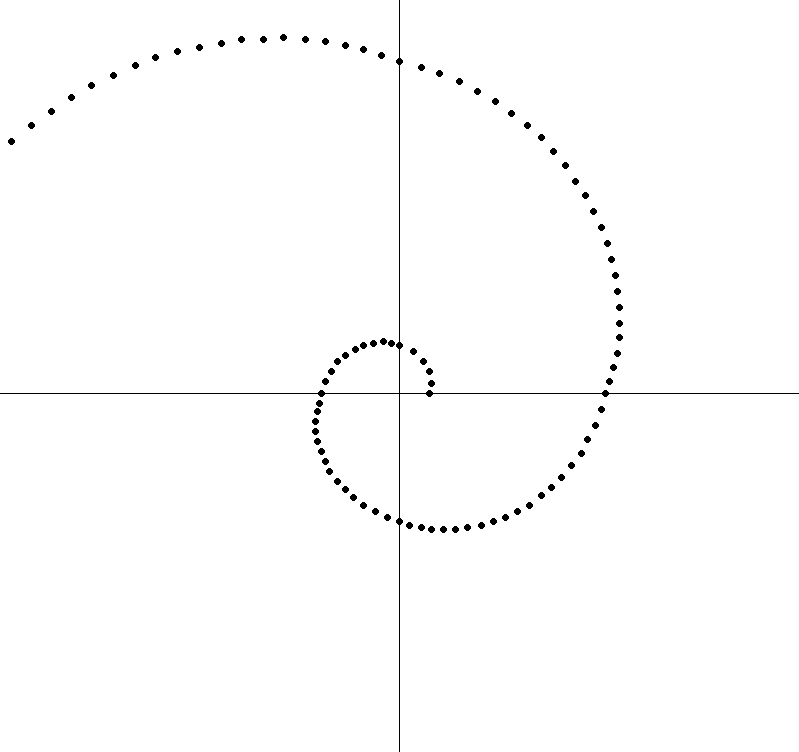
Note: After your program is working, try various initial positions and/or steps. Can you make the spiral look smother?