Information from: Perimeter of an Ellipse

Infinite Series Equation to Calculate an Ellipse's Perimeter

This is an exact equation. It requires an infinite number of terms to get the exact perimeter. With fewer terms, however, we can calculate a very close approximation.

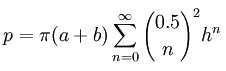
Step 1, calculate the ellipse's "h" value

Step 2, use the "infinite series" equation

This is the expand series with 4 terms. It shows terms n=0 to n=3 (1, 1/4, 1/64, 1/256).

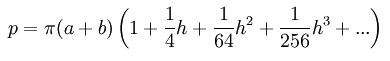
With more terms we get a more accurate answer.
the next term (n=4) is (25/16384)h⁴
the next term (n=5) is (49/65536)h⁵
the next term (n=6) is (441/1048576)h⁶
the next term (n=7) is (1089/4194304)h⁷

Note: For eccentricities less than 0.5 (h < 0.005), the error is at the limits of double-precision floating-point after the h⁴ term. In other words the precision of the hardware/software is exceeded.

The Binomial Coefficient Formula For The Infinite Series Equation Is

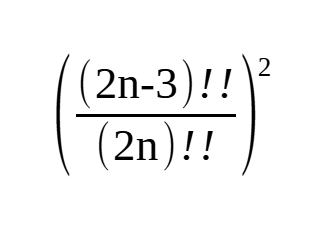
(In other words 1, 1/4, 1/64, 1/256, ...)