Hodgepodge

Introduction

The primary tool for estimating the distance to a Cepheid variable star is the distance modulus equation. It relates apparent (m) and absolute (M) magnitudes to distance (d) in parsecs. The equation is

m - M = 5log(d/10)

Rearranged it is

d = 10^(m-M+5)/5

the distance (in parsecs) to the Cepheid variable star.

FYI: Cepheid stars are variable stars that exhibit periodic changes in brightness due to pulsations in their size and temperature. These pulsations are typically regular, with periods ranging from a few days to a few months. Cepheids are particularly useful for measuring distances to galaxies because of the period-luminosity relationship, meaning that brighter Cepheids have longer periods.

Project #1

Create an interactive program to calculate the distance to Cepheid variable stars in parsecs and lightyears.

What data should the user enter? (Keep it simple.)

apparent and absolute magnitude?
period and apparent magnitude?

Test your code with the examples found HERE

and HERE

Project #2

Are Cepheid variable stars in the star catalog below? What data is available?

Project #3

Create a GUI for Project #1.

Links

Cepheid variable (Wikipedia)

Parsec (Wikipedia)

Edwin Hubble (Wikipedia)

How to Use Variable Stars to Calculate Distance in the Universe (YouTube)

Cepheid Variable Stars, Supernovae and Distance Measurement

Star Catalog

A location where you can download a star catalog ...

Yale Bright Star Catalog (9110 stars)

bsc5.dat.gz is the ASCII star catalog data file. (one star per line)

bsc5.readme is the star catalog description (includes the catalog data format).

Another star catalog download location ...

Bright Star Catalogue, 5th Revised Ed. : V/50 (9110 stars)

Extracting data from the catalog records (one line, one star) has some quirks. I suggest you look at Python slice strings. Slice strings are indexed starting with zero (0). The data description indexing starts with one (1). Also the slice string's starting index is inclusive and the ending index is exclusive.

For example

slice index	data description index
0	1
1	2
2	3
...	...

Hertzsprung-Russell Diagram

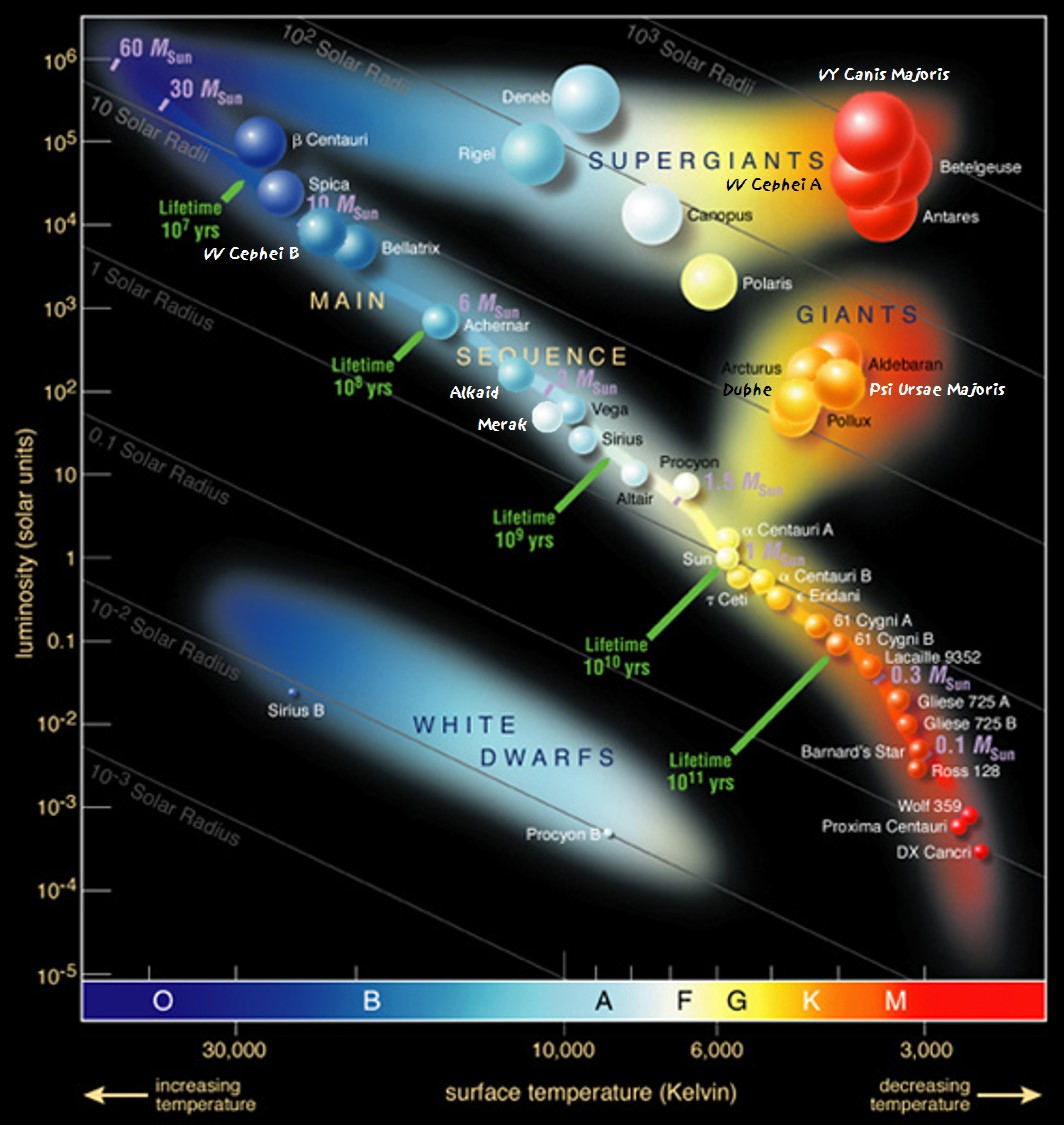
Image From: commons.wikimedia.org

FYI: For a large version of the Hertzsprung-Russell Diagram click HERE .

Using a Cepheid Variable Star's Period, Calculate its Absolute Magnitude

The absolute magnitude (M) of a Cepheid can be calculated using the following formula:

M = -2.43 * (log(P) - 1) - 4.05

Where:

M is the absolute magnitude
P is the period of the Cepheid in days