Introduction

What are we going to do here?

Practice Python3 programming using graphics transformation matrices as the focus.

Perspective will not be part of the projects. The viewer is assumed to be at +z infinity.

Perspective: In a realistic images, objects farther away appear smaller.

See possible programs and activities HERE .

See some possible projects HERE .

Purpose

Create programs that use a 2D or 3D transformations matrix. The instructor will give you the complete requirements for the class/project.

Description

In computer graphics, the major coordinate transformation are:

• Translation (move objects in the x,y,z directions)
• Rotation (rotate object around the origin's x,y,z axes)
• Scaling (make objects bigger or smaller)
• Convert from one coordinate system to another

For example, draw a 20x20 square centered on the origin (0,0 center of the window?). Rotate it 45° counterclockwise. Move it to coordinates 100,100. Shrink it to 1/2 its size.

Don't get nervous if you aren't into equations and all of that math-stuff. Code examples are provided to cut and paste. See "Test Code, Demo Code, ..." . For more detailed information (equations, math, etc.), see the links at the bottom of this page, or go HERE .

Graphics Program Structure (sort of)

A graphics program takes graphics objects (lines, circles, triangles, rectangles, ...) defined by coordinates and draw them in a window. For example:

1. define some graphics objects
2. creates a transformation matrix
3. using the matrix, translate, rotate, scale, ... graphics object coordinates
4. clear the window
5. in the window, draw graphics objects using the new coordinates
6. loop (rinse and repeat)

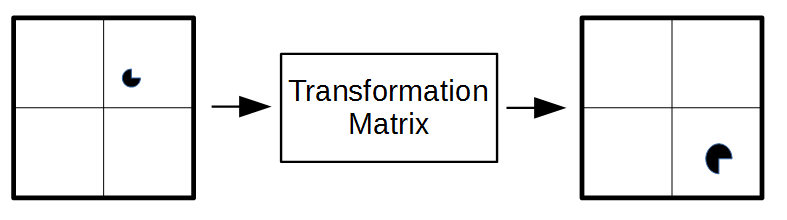
Do these steps fast enough and you have animation. Do these steps slowly and you can rotate data to view it from different angles.

Graphics Library

For the class, use graphics.py. It is a simple graphics library. Click HERE for more information. (download, install, documentation, ...)

One alternative to graphics.py is tkinter. Graphics.py is a wrapper around tkinter and is simpler to use. tkinter comes pre-installed in Python3, and is a more complex and capable graphics library. For more information about tkinter, go HERE .

Turtle (Linux KTurtle) and the Python module matplotlib are other possible graphics libraries.

(FYI: You don't need to know this to use it but... Tkinter is a set of Python bindings for TCL/TK.)

Code and Stuff

Test Code, Demo Code, ...

Program Design/Build Steps

2D Transformation Matrix

3D Transformation Matrix

Notes, Definitions, ...

Download/Install Linux/Python/IDE

Download/Install Linux
Download/Install Python

Note: You can use a standard text editor or you can download/install a Python IDE. There are many available on the web. (Search YouTube for "best python ide".)

Links

Computer Graphics Tutorial
Introduction to Computer Graphics: free, on-line textbook
Introduction to Computer Graphics: Transforms
2D Transformation
Transformation Matrices
Transform2D
Python Transformation Matrix
Rotate, Scale and Translate 2D Coordinates
Determining a Homogeneous Affine Transformation Matrix from Six Points in 3d USI
3D Programming In Python

Coordinate System

Right hand rule. The viewer is usually at +z infinity.

            +Y  -Z
            |  /
            | /
            |/
  -X -------+------- +X
           /|
          / |
         /  |
       +Z   -Y

Normal Vector

See "my normal vector" comments and code HERE .

The normal vector is a vector perpendicular to the plane formed by two vectors. It can be used to determine if a plane is visible to a viewer. If not, it does not need to be drawn (rendered). This can speed up a graphics program and use less resources by reducing the number of objects to draw.

How do I Use The Provided Normal Vector Support Function?

A normal vector support function can be found in the Test Code, Demo Code, ... section. It requires three point on a surface to do the calculations, but they must be in a specific clockwise order.

The easiest way to pick three points is to pick points that are used to define an object's edges.The points are selected in a clockwise direction from outside the solid object, looking down on the surface. For example, given the following points on an object's surface ...

    +-------------------------------+
    |                               |
    |  p0       p2            p5    |
    |                               |
    |       p4            p3        |
    |                               |
    |            p6                 |
    |                               |
    +-------------------------------+

Create a clockwise list of 3 points ...

Curl your left hand fingers (clockwise) over the surface. The thumb indicates which direction the normal vector points.