#! /usr/bin/python3 # ============================================================ # 1. test graphics transformations # 2. manipulate/draw a cube's surfaces (polygons) # 3. test using a normal vector for each surface to determine # if a surface is visible to the viewer. If not, do not # render (draw) it. # # ============================================================ import coordinate_conversion as cc import transformation_matrix as tm import user_interface as ui from graphics import * import numpy as np import sys WINHEIGHT = 801 # graphics window height WINWIDTH = 801 # graphics window width PEEK = True # ------------------------------------------------------------ # ---- cube # ---- # ---- notes: # ---- 1. Cartesian coordinates # ---- 2. coordinates are of a size so they do not need to be # ---- scaled to fit in the graphics window # ---- 3. the pivot point coordinates are the center of a # ---- graphics object and is used when rotating it's # ---- wireframe in place (not needed at the origin) # ------------------------------------------------------------ # ---- cube 8 surface's corner points pts = [ (-100, 100, 100), (-100, 100,-100), ( 100, 100,-100), ( 100, 100, 100), (-100,-100, 100), (-100,-100,-100), ( 100,-100,-100), ( 100,-100, 100) ] # ---- cube's pivot point PIVOT_POINT = (0, 0, 0) # ---- cube 6 surfaces # ------ 0 top # ------ 1 bottom # ------ 2 back # ------ 3 front # ------ 4 left # ------ 5 right # ---- surface points are in clockwise order as viewed # ---- from outside the cube. they define a flat surface. # ---- surface fields are: surface points, surface color, # ---- surface name CUBE_SURFACES = [ ((pts[0],pts[1],pts[2],pts[3]), # top 'red','top'), ((pts[4],pts[7],pts[6],pts[5]), # bottom 'blue','bottom'), ((pts[1],pts[5],pts[6],pts[2]), # back 'black','back'), ((pts[0],pts[3],pts[7],pts[4]), # front 'green','front'), ((pts[0],pts[4],pts[5],pts[1]), # left 'yellow','left'), ((pts[3],pts[2],pts[6],pts[7]), # right 'cyan','right')] # ============================================================ # Three points can define a plane. If they do, you can # calculate a vector perpendicular to the plane. If the points # do not form a plane the cross product vector is [0,0,0]. # # The vector can be used to determine if a plane is facing # the viewer or not. With solid object made up of thousands # surfaces, you can determine which surfaces need to be # rendered and which ones do not. This can make rendering the # object more efficient. You don't need to draw all of the # triangles. # ============================================================ def calc_cross_product(p1,p2,p3,verbose=False): if verbose: print('calc_cross_product()') print(f'p1 = {p1}') print(f'p2 = {p2}') print(f'p3 = {p3}') # ---- get two vectors in the plane relative to point p1 v1 = [p3[0]-p1[0],p3[1]-p1[1],p3[2]-p1[2]] v2 = [p2[0]-p1[0],p2[1]-p1[1],p2[2]-p1[2]] if verbose: print(f'v1 = {v1}') print(f'v2 = {v2}') # ---- the cross product is a vector perpendicular # ---- to the plane cp = np.cross(v1,v2) if verbose: x = cp[0] y = cp[1] z = cp[2] print(f'cross product = [ x={x},y={y},z={z} ]') return cp # ------------------------------------------------------------ # ---- XYZ 3D axes # ---- # ---- notes: # ---- 1. Cartesian coordinates # ---- 2. the origin (0,0,0) is the center of the # ---- graphics window # ------------------------------------------------------------ AXES = (((-300,0,0),(300,0,0)), # X axis ((0,-300,0),(0,300,0)), # Y axis ((0,0,-300),(0,0,300))) # Z axis # ------------------------------------------------------------ # ---- class - 3D transformation matrix # ---- # ---- notes: # ---- 1. Cartesian coordinates # ------------------------------------------------------------ class TransformationMatrix3D: # ---- initialize the class (create an identity matrix) def __init__(self): self.mtrx = np.identity(4) #---- reset matrix to initial condition def reset(self): self.mtrx = np.identity(4) # ---- transform a point's coordinates using the # ---- transformation matrix def transform_coords(self,x,y,z): p = self.mtrx @ [x,y,z,1] return (p[0],p[1],p[2]) # ---- modify transformation matrix # ---- change the location (coordinates) of a point # ---- Note: DX,DY,DZ are the change in a point's # ---- current X,Y,Z coordinates def translate_to_location(self,dx,dy,dz): m = tm.get_translation_matrix_3d(dx,dy,dz) mm = m @ self.mtrx self.mtrx = mm # ---- modify transformation matrix # ---- move a point to the origin (0,0,0) # ---- Note: X,Y,Z are a point's current # ---- location (coordinates) def translate_to_origin(self,x,y,z): m = tm.get_translation_matrix_3d(-x,-y,-z) mm = m @ self.mtrx self.mtrx = mm # ---- modify transformation matrix # ---- rotate around the X axis def rotate_around_x_axis(self,degrees): m = tm.get_x_rotation_matrix_3d(degrees) mm = m @ self.mtrx self.mtrx = mm # ---- modify transformation matrix # ---- rotate around the Y axis def rotate_around_y_axis(self,degrees): m = tm.get_y_rotation_matrix_3d(degrees) mm = m @ self.mtrx self.mtrx = mm # ---- modify transformation matrix # ---- rotate around the Z axis def rotate_around_z_axis(self,degrees): m = tm.get_z_rotation_matrix_3d(degrees) mm = m @ self.mtrx self.mtrx = mm # ---- modify transformation matrix # ---- scale a point's coordinates in the X,Y,Z direction def scale_xyz(self,sx,sy,sz): m = tm.get_scaling_matrix_3d(sx,sy,sz) mm = m @ self.mtrx self.mtrx = mm # ---- return a deepcopy of the current # ---- transformation matrix def deepcopy_matrix(self): return copy.deepcopy(self.mtrx) # ---- return a shallow copy of the current # ---- transformation matrix def copy_matrix(self): return self.mtrx # ---- display the current transformation matrix def display_matrix(self): print(self.mtrx) # ------------------------------------------------------------ # ---- draw XYZ 3D axes # ---- # ---- Note: # ---- 1. axes Cartesian coordinates # ---- 2. the origin (0,0,0) is assumed to be at the center # ---- of the graphics window # ---- 3. viewer is assumed to be at +Z infinity # ------------------------------------------------------------ def draw_xyz_axes(win, mtrx, axes, width=2, color='black', draw_z_axis=False): axis_objs = [] # ---- draw X axis (line) xaxis = axes[0] x0 = cc.center_to_win_coords(xaxis[0][0],xaxis[0][1], win.width,win.height) x1 = cc.center_to_win_coords(xaxis[1][0],xaxis[1][1], win.width,win.height) lobj = Line(Point(x0[0],x0[1]),Point(x1[0],x1[1])) lobj.setWidth(width) lobj.setFill(color) lobj.draw(win) axis_objs.append(lobj) # ---- draw Y axis (line) yaxis = axes[1] y0 = cc.center_to_win_coords(yaxis[0][0],yaxis[0][1], win.width,win.height) y1 = cc.center_to_win_coords(yaxis[1][0],yaxis[1][1], win.width,win.height) lobj = Line(Point(y0[0],y0[1]),Point(y1[0],y1[1])) lobj.setWidth(width) lobj.setFill(color) lobj.draw(win) axis_objs.append(lobj) # ---- draw Z axis (line) if draw_z_axis: zaxis = axes[2] z0 = cc.center_to_win_coords(zaxis[0][0],zaxis[0][1], win.width,win.height) z1 = cc.center_to_win_coords(zaxis[1][0],zaxis[1][1], win.width,win.height) lobj = Line(Point(z0[0],z0[1]),Point(z1[0],z1[1])) lobj.setWidth(width) lobj.setFill(color) lobj.draw(win) axis_objs.append(lobj) return axis_objs # ------------------------------------------------------------ # ---- draw graphics window 2D axes # ---- # ---- Note: # ---- 1. the origin (0,0,0) is assumed to be at the center # ---- of the graphics window # ---- 2. no Z axis drawn # ---- viewer is assumed to be at +Z infinity # ------------------------------------------------------------ def draw_graphics_window_axes(win, width=1 , color='black', labels=False): wx = win.width # window width wy = win.height # window height wcx = round(wx/2.0) # window center X wcy = round(wy/2.0) # window center Y axis_objs = [] # ---- X axis xl = Line(Point(0,wcy),Point(wx-1,wcy)) xl.setWidth(width) xl.setFill(color) xl.draw(win) axis_objs.append(xl) if labels: txt = Text(Point(wx-20,wcy),'X') txt.setFace('courier') txt.setSize(24) txt.setTextColor(color) txt.draw(win) axis_objs.append(txt) # ---- Y axis yl = Line(Point(wcx,0),Point(wcx,wy-1)) yl.setWidth(width) yl.setFill(color) yl.draw(win) axis_objs.append(yl) if labels: txt = Text(Point(wcx,20),'y') txt.setFace('courier') txt.setSize(24) txt.setTextColor(color) txt.draw(win) axis_objs.append(txt) return axis_objs # ------------------------------------------------------------ # ---- create a polygon (4 points) (X,Y,Z Cartesian coords) # ---- viewer is at +Z infinity, no Perspective adjustment # ------------------------------------------------------------ def create_polygon(win, mtrx, surface_points, width=2, color='green', draw_obj=True): # ---- convert Cartesian coords to window coords window_polygon_points = [] for pt in surface_points: wx,wy = cc.center_to_win_coords(pt[0],pt[1], win.width,win.height) # ---- save list of points window_polygon_points.append(Point(wx,wy)) # ---- create polygon graphics object pobj = Polygon(window_polygon_points) pobj.setOutline('black') pobj.setWidth(width) pobj.setFill(color) if draw_obj: pobj.draw(win) return pobj # return polygon graphics object # ------------------------------------------------------------ # ---- draw surfaces (Cartesian coordinates) # ---- viewer is at +Z infinity, no Perspective adjustment # ------------------------------------------------------------ def draw_surfaces(win,mtrx,surfaces): polygon_objs = [] for surface in surfaces: # ---- modify surface point's Cartesian coordinates # ---- using transformation matrix new_polygon_pts = [] for pt in surface[0]: new_pt = mtrx.transform_coords(pt[0], # x pt[1], # y pt[2]) # z new_polygon_pts.append(new_pt) # ---- draw the surface? # ---- determined by the surface's normal vector # ---- can the viewer see the surface? cp = calc_cross_product(new_polygon_pts[0], # pt 0 new_polygon_pts[1], # pt 1 new_polygon_pts[2]) # pt 2 if PEEK: print('-'*60) print(f'surface {surface[2]:6}') print(f'normal vector {cp}') # ---- create/draw a surface? if cp[2] > 0: if PEEK: print(f'draw color={surface[1]}') pobj = create_polygon(win,mtrx,new_polygon_pts, color=surface[1]) polygon_objs.append(pobj) else: if PEEK: print(f'do not draw (color={surface[1]})') return polygon_objs # ------------------------------------------------------------ # ---- delete graphics objects from graphics window # ------------------------------------------------------------ def clear_graphics_window(objs): for o in objs: o.undraw() objs = [] # ------------------------------------------------------------ # ---- menu interface # ------------------------------------------------------------ def menu_interface(): extra_menu_items = False menu = ''' ------------------------------------------------ ---------- test Transformation Matrix ---------- 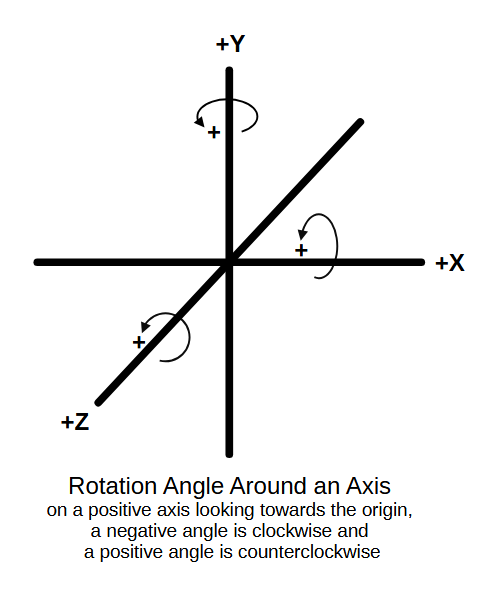Negative rotation angles rotate objs clockwise. Positive angles rotate objs counterclockwise. DX, DY, DZ are changes in an obj's current location, not an absolute location. ------------------------------------------------ q = quit i = reset to initial conditions d = draw cub surfaces m = display transformation matrix c = clear the graphics window (undraw) --------- Build Transformation Matrix ---------- rx angle = rotate around X axis (deg) ry angle = rotate around Y axis (deg) rz angle = rotate around Z axis (deg) t dx dy dz = move graphics object s sx sy sz = scale graphics object''' extra_menu = ''' o move to origin rip rotate in place all display extra menu options''' # ---- menu support function - oops! def _oops(s): print() print(f'OOPS! unknown/bad command ({s})') ui.pause() # ---- graphics object lists ax_objs = [] # axis graphics objects gr_objs = [] # other graphics objects # ---- create graphics window win = GraphWin('wireframe Transformation Test', WINWIDTH, WINHEIGHT) win.setBackground('white') # ---- create X,Y,Z coordinate transformation matrix mtrx = TransformationMatrix3D() # ---- draw X,Y,Z coordinate axes ##ax_objs = draw_xyz_axes(win,mtrx,AXES) ax_objs = draw_graphics_window_axes(win) # ---- display the menu # ---- ask the user to make a selection # ---- process the selection while True: ##ui.clear_screen() print(menu) if extra_menu_items: print(extra_menu) # ---- ask the user to make a selection print() s = ui.get_user_input('Enter command: ') if not s: break # empty string? # ---- lowercase the user's input ss = s.lower() # ---- quit if ss[0] == 'q': break # ---- display transformation matrix if ss[0] == 'm': print('-'*44) mtrx.display_matrix() print('-'*44) ui.pause() continue # ---- create/draw surfaces if ss[0] == 'd': objs = draw_surfaces(win,mtrx,CUBE_SURFACES) gr_objs += objs continue # ---- reset matrix to initial state if ss[0] == 'i': mtrx.reset() continue # ---- clear graphics window if ss == 'c': ##clear_graphics_window(ax_objs) clear_graphics_window(gr_objs) continue # ---- add rotation to transformation matrix if ss[0] == 'r': x = ss.replace(',', ' ').split() if len(x) != 2: _oops(s) continue tf,deg = ui.is_float(x[1]) if not tf: _oops(s) continue if x[0][1] == 'x': print('rotate around X axis') mtrx.rotate_around_x_axis(deg) continue if x[0][1] == 'y': print('rotate around Y axis') mtrx.rotate_around_y_axis(deg) continue if x[0][1] == 'z': print('rotate around Z axis') mtrx.rotate_around_z_axis(deg) continue # ---- add X,Y,Z movement to transformation matrix if ss[0] == 't': x = ss.replace(',', ' ').split() if len(x) != 4: _oops(s) continue tf,dx = ui.is_float(x[1]) # DX if not tf: _oops(s) continue tf,dy = ui.is_float(x[2]) # DY if not tf: _oops(s) continue tf,dz = ui.is_float(x[3]) # DZ if not tf: _oops(s) continue mtrx.translate_to_location(dx,dy,dz) continue # ---- move to origin if ss[0] == 'o': print('exercise for the student') continue # ---- rotate in place if ss[0] == 'rip': print('exercise for the student') continue # ---- toggle the display of extra menu items if ss == 'all' or ss == 'extra': extra_menu_items = not extra_menu_items continue # ---- OOPS! _oops(s) # ---- close graphics window win.close() # ------------------------------------------------------------ # ---- main # ------------------------------------------------------------ if __name__ == '__main__': menu_interface() print()