Disclaimer

I don't clam this is good code or a good algorithm or good for anything in particular. I'm sure that someone previously came up with the same "stuff". It is me just playing around with code. Take it for what it is.

Result Summary

I hypothesized that shuffling a few nodes during node insertion could make a binary search tree faster by shorting the number of levels (see diagrams below).

There are two different ways of applying my algorithm. btree_9 applies the algorithm on each new node as it is inserted in a tree. btree_a applies the algorithm after the tree is built.

The results of creating the code and testing it is that btree_9 does not work. btree_a, however, can make slight improvements in some cases, but in a few cases it make things slightly worse. (See the code/documentation/diagrams below.)

After seeing that the first hypothesis did not work in many cases, I hypothesized that perhaps the number of nodes in the tree had some effect (small tree vs large tree). This also did not work.

The results of testing various tree sizes indicated the following:

The result of various tree sizes (number of nodes) appears to be random good and bad. In general shuffling nodes does not make things better. In fact, it can make things much worse.

It was however fun playing with the code.

Introduction

This is me playing around with binary search trees.

Depending on the order of the incoming data, a tree can become very un-balanced, awkward, and slow searches down.

I was thinking, "How can I ameliorate really bad trees?". My code will not build a perfect binary tree, but perhaps build a tree that would speed up searches (a shallower, not as deep, tree). It would also be great if this was done at tree build time rather than after the fact. (This could be described as "build seldom" and "search often" data usage.)

Sure I could Google "stuff" (algorithms, etc.), but that's no fun. I wanted to see if I could come up with something. That is why the title is "A Sort of Balanced Binary Trees".

The following diagram shows a "bad" binary tree. As you can see it is much deeper that it needs to be.

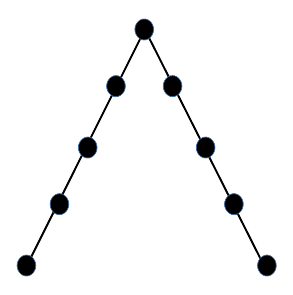
I am hoping that my code will ameliorate the worst cases. If not, it was fun playing around with binary trees.

The code is not as compact as it could be, but hopefully it is easier to read and understand.

Also, there is code commented out. This code is "I tried out code" or "what if code" or "debugging code" or ... Remove it if you want.

By the way, I am using Python 3.

Node Class Definition

class Node:
    def __init__(self, data):
        self.data    = data
        self.left    = None
        self.right   = None
        self.parent  = None

    def PrintNode(self,title='',single_line = True):
        d = 'None' if self.data   == None else self.data
        l = 'None' if self.left   == None else self.left.data
        r = 'None' if self.right  == None else self.right.data
        p = 'None' if self.parent == None else self.parent.data
        if title: print(title)
        if single_line:
            print('(d={},l={},r={},p={})'.format(d,l,r,p))
        else:
            print('data   = {}'.format(d))
            print('left   = {}'.format(l))
            print('right  = {}'.format(r))
            print('parent = {}'.format(p))

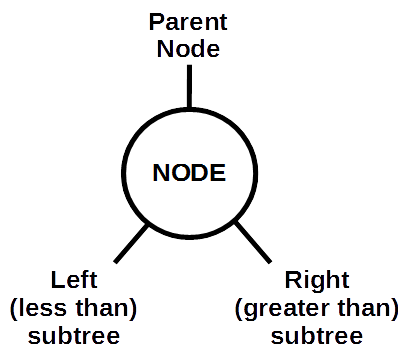
You should know several things about the Node class definition

• All of the tree functionality is in the BinaryTree class, not in the Node class.
• The user has the responsibility for creating and populating nodes.
• All nodes have a parent node except the root node. It is set to None.
• The left subtree contains nodes less than the subtree's root node.
• The right subtree contains nodes greater than the subtree's root node.

BinaryTree Class Definition

class BinaryTree:

    def __init__(self):
        self.root    = None
        self.balance = False
        self.debug   = False

    .... tree functions not show here ....
    .... see the link  below          ....

You should know several things about the BinaryTree class definition

• There is no root node in the beginning. The first node inserted into the tree becomes the root node.
• All of the tree functionality is in the BinaryTree class.
• The user has the responsibility for creating and populating nodes.
• Malformed nodes can be inserted into the tree.
• Currently duplicates nodes are not allowed. You can change this.
• The first node inserted into the tree becomes the tree's root node. This is not a problem because the resultant tree that is created is not perfectly symmetrical.

Diagrams

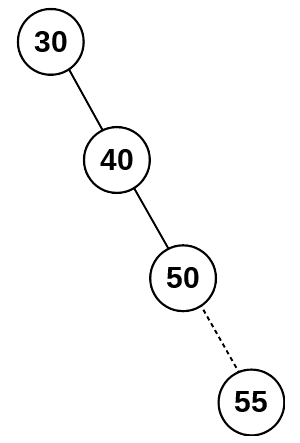
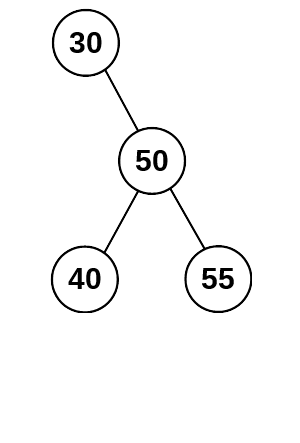
As you can see in the diagrams below, adding node 55 will make the depth of the right subtree longer. However, if node 50 has an empty left subtree, the nodes can be shuffled to keep the subtrees the same depth. The shuffling can be done when node 55 is inserted into the tree as part of the insert process.

Insert Node 55

After Balancing

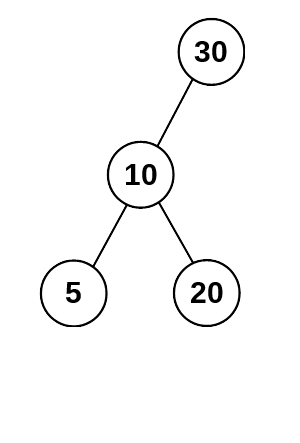
As you can see in the diagrams below, adding node 5 will make the depth of the left subtree longer. However, if node 10 has an empty right subtree, the nodes can be shuffled to keep the subtrees the same depth. The shuffling can be done when node 5 is inserted into the tree as part of the insert process.

Insert Node 5

After Balancing

Pseudo Code

Files

btree_9 tries to balance a new node's child nodes when the new node is inserted into the tree.

btree_a tries to balance a tree after the tree is create.